矛盾律是逻辑学中的基本原理之一，它揭示了在同一逻辑体系中，某个命题与其否定命题不能同时为真，在实际应用中，我们常常会遇到一些看似矛盾却又合理的现象，本文将通过“百度一下”的方式，探寻矛盾律的例子，揭示逻辑悖论的奥秘。

矛盾律的定义

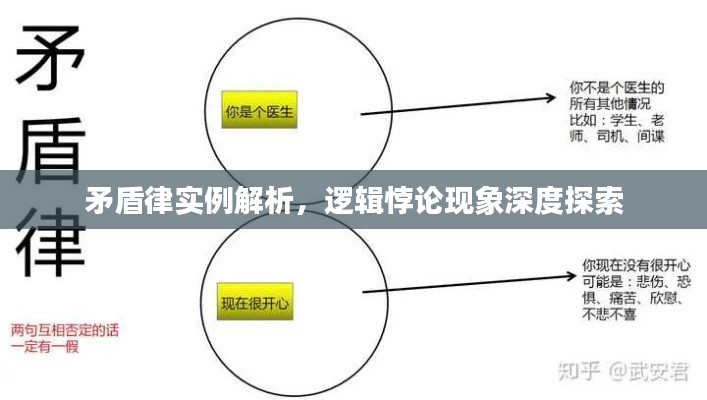
矛盾律，又称不矛盾律，是形式逻辑的基本规律之一，它要求在同一思维过程中，两个相互矛盾或反对的命题不能同时为真，换句话说，如果一个命题是真的，那么它的否定命题必须是假的。

矛盾律的应用实例

通过百度搜索，我们可以找到许多与矛盾律相关的实例，以下是一些典型的例子：

1、著名的“理发师悖论”

在一个村子里，有一位理发师，他只为那些不给自己剪头发的人剪头发，问题是：这位理发师是否应该给自己剪头发？如果他不给自己剪，那么按照他的规则，他应该给自己剪；但如果他给自己剪，那就违反了他的规则。

2、集合论中的自指悖论

假设有一个集合，它包含所有不包含自己的集合，那么这个集合是否包含自己？如果它包含自己，那么它就违反了自己的定义；如果它不包含自己，那么它就符合自己定义中的条件，应该包含自己，这就是著名的罗素悖论。

矛盾律的逻辑悖论分析

上述例子揭示了矛盾律在实际应用中的复杂性，这些看似矛盾的现象实际上是逻辑悖论的一种表现，逻辑悖论是指在形式逻辑系统中，某些命题或推理在表面上看似合理，但却导致自相矛盾的结果，这些悖论挑战了我们的思维方式和逻辑系统。

如何解决逻辑悖论？

解决逻辑悖论需要深入分析和理解矛盾产生的根源，有以下几种方法：

1、完善定义：重新审视和修正导致悖论的定义或前提，以避免自相矛盾的情况。

2、引入新的概念或原则：通过引入新的概念或原则来化解矛盾，例如采用更严格的逻辑系统或公理体系。

3、限制应用范围：明确逻辑系统的适用范围和条件，避免将逻辑规则应用于不适用的领域。

矛盾律是逻辑学中的基本原理，但在实际应用中，我们常常会遇到逻辑悖论的现象，通过探索矛盾律的例子，我们可以更好地理解逻辑悖论的奥秘和挑战，解决逻辑悖论需要深入分析和理解矛盾产生的根源，并寻求合适的方法来化解矛盾，希望本文能够帮助读者更好地理解矛盾律和逻辑悖论，提高逻辑思维能力。

（注：本文所提到的例子和解析仅为示意性质，实际矛盾律的应用和解析可能更为复杂。）在未来的研究中，我们还需要进一步探讨矛盾律与其他逻辑原理的关系，以及如何更好地将逻辑学应用于实际生活中，以解决复杂的逻辑问题。